1. Сигналы в системах передачи

Существует много различных способов передачи сигналов. Так, два человека могут "связываться" между собой, пользуясь речью, жестами или графическими символами. В далеком прошлом передача на большие расстояния осуществлялась с помощью звуковых сигналов, барабана, дыма костра, почтовых голубей и световых лучей. Теперь связь на большие расстояния реализуется в основном с помощью электрических и оптических сигналов. Объясняется это тем, что сигналы данного вида можно передавать на огромные расстояния (теоретически на любые расстояния в пределах Вселенной) с очень большой скоростью (около 3х10 8 м/с).

Связь представляет собой процесс передачи сообщений от источника к получателю. Сообщением называют совокупность сведений о состоянии какого-либо материального объекта. Источник и получатель сообщений разделены некоторой средой, в которой источник образует возмущения, отображающие сообщение и воспринимаемые получателем.

Физическая реальность, изменения которой в пространстве и во времени отображают передаваемое сообщение, называется сигналом. Например, при разговоре источником сообщений является голосовой аппарат человека, в качестве сигнала выступает изменяющееся в пространстве и во времени воздушное давление - акустические волны; получателем служит человеческое ухо.

В современном обществе для передачи различного рода сообщений широко используются электрические сигналы - электромагнитные колебания, изменения параметров которых отображают передаваемые сообщения. Электрические сигналы имеют ряд преимуществ перед сигналами другой физической природы - они могут передаваться на весьма большие расстояния, их форму можно преобразовывать сравнительно простыми техническими средствами, скорость их распространения близка к скорости света. Передача, излучение и прием сообщений по электромагнитным системам называется электросвязью.

Существуют различные виды электросвязи - телефония, видеотелефония, телеграфия, передача данных и др. Комплекс технических средств, обеспечивающих передачу сигналов электросвязи, называется системой электросвязи. В пункте передачи такой системы сигналы неэлектрической природы, порождаемые источником сообщений, должны быть преобразованы в электрические сигналы; в пункте приема должно происходить обратное преобразование электрических сигналов в сигналы, воспринимаемые получателем. При этих преобразованиях должно соблюдаться взаимное соответствие между каждым из возможных сообщений и электрическим сигналом, переносящим это сообщение. Таким образом система электросвязи представляет собой комплекс разнообразных и, зачастую, весьма сложных, взаимодействующих между собой электротехнических и радиоэлектронных устройств, предназначенных для формирования, передачи и приема электромагнитных сигналов, переносящих сообщения любого вида. При передаче сигналы искажаются вследствие несовершенства (неидеальности характеристик) технических устройств; кроме того, на сигналы накладываются помехи, являющиеся сторонними возмущениями различного происхождения и мешающие точному воспроизведению сообщения у получателя.

Системы передачи сигналов должны быть построены так, чтобы, несмотря на искажения и помехи, сообщение восстанавливалось с заданной точностью.

1.1. Аналоговые, дискретные и цифровые сигналы

Аналоговым сигналом в системах передачи называется непрерывный электрический или оптический сигналы F н (t), параметры которого (амплитуда, частота или фаза) изменяются по закону непрерывной функции времени источника информации, например, речевого сообщения, подвижного или неподвижного изображения и т. д. Непрерывные сигналы могут принимать любые значения (бесконечное множество) в некоторых пределах (рисунок 1.1).

Рисунок 1.1. Аналоговый непрерывный сигнал.

Дискретные сигналы - состоят из отдельных элементов, принимающих конечное число различных значений. Аналоговые дискретные сигналы F д (t) можно получить из непрерывных F н (t), используя дискретизацию по времени (через интервал Т д), квантование по амплитуде (через интервал (?) или их одновременно (рисунок 1.2 а, б, в). Цифровой сигнал F ц (t) формируется в виде группы импульсов в двоичной системе счисления, соответствующих амплитуде квантованного по уровню и дискретного по времени аналогового сигнала (рисунок 1.2г), при этом наличие электрического импульса соответствует "1" в двоичной системе счисления, а отсутствие - "0". Основным преимуществом цифровых сигналов является высокая помехозащищенность, так как при наличии шумов и искажений при их передаче достаточно зарегистрировать на приеме наличие или отсутствие импульсов.

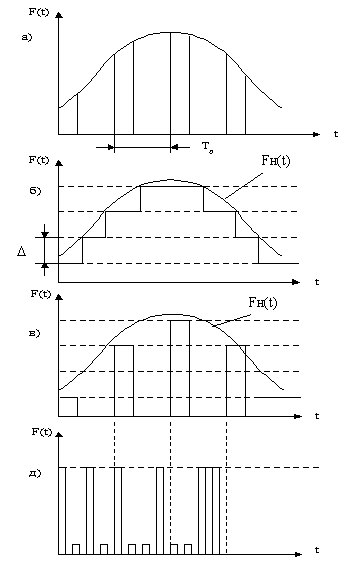
а) - дискретный по времени; б) - дискретный по уровню;

в) - дискретный по времени и по уровню; г) - цифровой двоичный сигнал.

Преобразование непрерывного сигнала в цифровой может осуществляться при помощи импульсно - кодовой модуляции, дельта - модуляции, дифференциальной импульсно - кодовой модуляции (ИКМ, ДМ, ДИКМ) и их модификаций. Таким образом, для получения цифрового сигнала принципиально необходимо произвести три основные операции над непрерывным сигналом: дискретизацию по времени, квантование по уровню и кодирование.

1.2. Многоканальные системы передачи

Многоканальной системой передачи называется совокупность технических средств, обеспечивающих одновременную и независимую передачу сообщений от нескольких источников к получателям по одной линии передачи. К передатчику N-канальной системы связи подводятся первичные сигналы от N источников сообщений. Эти первичные сигналы подвергаются специальной обработке, (преобразуются в канальные сигналы), затем объединяются в общий групповой сигнал, направляемый в линию передачи. В приемной части системы из группового сигнала выделяются индивидуальные сигналы отдельных каналов, соответствующие первичным передаваемым сообщениям. При построении многоканальных систем передачи одной из основных является задача разделения канальных сигналов. Для решения этой задачи требуется осуществить операцию преобразования первичных сигналов, состоящую в том, что в передающей части системы сигналы отдельных каналов наделяются некоторыми, заранее обусловленными признаками, которые должны быть такими, что бы в приемной части системы сигналы могли быть различены и разделены. Структурная схема такой системы N-канальной связи представлена на рисунке 1.3. Первичные сигналы c 1(t) , c 2 (t),..., c N (t), поступающие в передающую часть системы, преобразуются устройствами М 1 , М 2 ,..., М N ; сигналы на выходах этих устройств v 1 (t), v 2 (t), ... , N (t) называются канальными. Для аналитического описания этого преобразования введем в рассмотрение операторы(Оператор – математическое понятие, означающее соответствие между элементами двух множеств X и Y, относящее каждому элементу x множества X некоторый элемент у множества Y. Например,) M i, i=1,N, связывающие входные c i (t) и выходные v i (t) сигналы преобразователей M i . Теперь можно записать

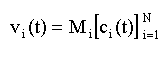(1.1.)

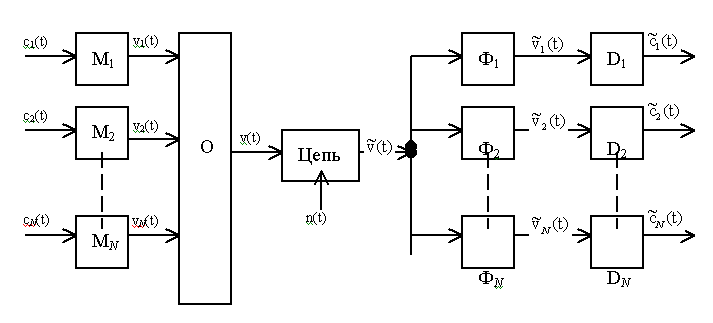
Рисунок 1.3. Структурная схема многоканальной системы передачи

с i (t) - первичные сигналы; M i - преобразователи, формирующие канальные сигналы; v i (t) - канальные сигналы; О - устройство объединения канальных сигналов; v(t) - групповой сигнал; n(t) - помеха; Ф i (t) - разделительные (фильтрующие) устройства; D i - преобразователи, восстанавливающие первичные сигналы.В процессе преобразования (1.1) необходимо решить две задачи. Во - первых, каждый из канальных сигналов v i (t), i=1,N нужно наделить совокупностью физических признаков

(первый индекс - номер признака, второй - номер канала), отличающих его от остальных канальных сигналов; эти признаки (или параметры) можно назвать разделительными. Во - вторых, необходимо сформировать канальные сигналы так, чтобы в них содержались передаваемые сообщения, то есть сведения о форме первичных сигналов, поступающих на входы каналов. Групповой сигнал v(t) получается объединением канальных сигналов. Обозначим оператор через О. Тогда

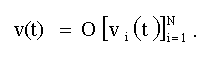(1.2)

В частности, групповой сигнал можно получить суммированием канальных сигналов

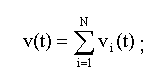(1.3)

такие системы назовем аддитивными. Системы, в которых для формирования группового сигнала применяются другие операции (не суммирование), будем называть комбинационными. В современной многоканальной связи используют в большинстве случаев аддитивные системы. Групповой сигнал, проходя через элементы системы передачи, претерпевает искажения - линейные и нелинейные; кроме того, на сигнал накладываются помехи. Поэтому сигнал, поступающий на вход приемной части системы, отличается от сигнала v(t). Введем следующие обозначения: - сигнал на входе приемной части системы; L - оператор, характеризующий линейные искажения; Z - оператор, характеризующий нелинейные искажения; n(t) - аддитивная помеха. Если искажения малы, то есть мало отклонение от v(t), то цепь можно представить в виде параллельного соединения двух четырехполюсников. Один из них вносит только линейные искажения, то есть характеризуются оператором L; другой создает только нелинейные искажения и характеризуется оператором Z. Тогда

(1.4)

Оператор L можно представить следующим образом. Если известна импульсная реакция цепи g L (t), то, используя интеграл Дюамеля, получим

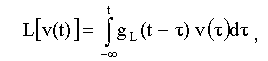(1.5)

Если задана комплексная частотная характеристика (передаточная функция) цепи H L (?), то, обозначая спектр группового сигнала черезSv(?), получим спектр сигнала на выходе цепи

Переходя от спектра к функции времени, то есть применяя обратное преобразование Фурье, находим

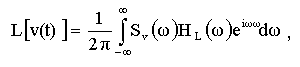(1.6)

Если линейных искажений нет, то H L ()=1 и L=v(t).

Выражения (1.5) и (1.6) характеризуют систему с постоянными параметрами (непараметрическую). Если параметры системы меняются во времени, то есть имеют место мультипликативные помехи, то импульсная реакция имеет вид g L (t,?), а передаточная функция H i (,т).Оператор Z можно представить в различной форме. Одно из наиболее часто встречающихся представлений имеет вид

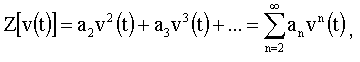(1.7)

При отсутствии нелинейных искажений все a n =0 и Z=0.

Перейдем к описанию работы приемной части системы передачи. Обозначим через Ф i операторы разделения (фильтрации) и через i (t) сигналы на выходах разделителей. С учетом этих обозначений

(1.8)

Разделяющие (фильтрующие) устройства в приемнике могут быть как линейными, так и нелинейными четырехполюсниками: соответственно, операторы Ф i будут линейными или нелинейными. Система передачи называется линейной, или системой с разделением каналов, если разделяющие устройства линейны; в противном случае система называется нелинейной.Восстановление первичных сигналов производится при помощи устройства D i . Вводя соответствующие операторы и обозначая через сигналы на выходах каналов, получим

(1.9)

Ясно, что чем меньше сигнал на выходе i - го канала отличается от сигнала ci(t) на его входе, тем выше качество связи. Целесообразно ввести некоторую численную оценку качества связи - некоторый критерий верности передачи, представляющий собой функционал от разности сигналов на входе и выходе канала:

(1.10)

Этот критерий, то есть вид функционала F, определяется теми требованиями, которые предъявляются к передаче данного вида сообщений. Так, например, при передаче аналоговых (непрерывных) сообщений часто применяют критерий среднеквадратического отклонения:

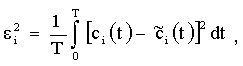(1.11)

где Т - длительность сигнала. При передаче дискретных сообщений критерием верности обычно служит вероятность ошибки? = рош, то есть вероятность неправильного восстановления переданного символа. Такие способы оценки называются прямыми. Возможен и другой подход к оценке качества связи - по характеристикам и параметрам каналов: частотным, амплитудной величине уровня помех и так далее. Такая оценка называется косвенной. Косвенные методы оценки более удобны в эксплуатации и поэтому широко применяются на практике. Прямые методы, как правило, более удобны в теоретических исследованиях. Теперь можно определить основные задачи теории и техники многоканальной связи. При исследовании и разработке многоканальных систем связи обычно известны свойства первичных сигналов, количество каналов системы и характеристики линии связи и помех, то есть операторы L и Z и статистические характеристики помехи n(t). Теория многоканальной связи должна указать класс канальных сигналов, обеспечивающих принципиальную возможность их разделения, и определить вид операторов М, О, Ф и D, то есть свойства преобразователей передачи и приема и фильтрующих устройств. Задача проектирования (разработки) многоканальной системы состоит подборе класса канальных сигналов и операторов М, О, Ф, и D, минимизирующих отклонение от с i (t) с точки зрения принятого критерия верности. Должны быть также указаны пути технической реализации соответствующих устройств. В системах многоканальной связи кроме внешних помех возникают специфические внутренние помехи: вследствие неидеальности цепей и аппаратуры полное разделение канальных сигналов оказывается невозможным, появляются взаимные переходные влияния между каналами. Необходимо указать пути снижения этих влияний до допустимых значений. Далеко не всегда удается решить задачу проектирования (разработки) многоканальной системы связи в такой общей постановке. Часто, вследствие сложности, ее решают по частям - сначала выбирают класс канальных сигналов, операторы их формирования М i и оператор объединения О, а затем, полагая известными свойства группового сигнала, находят операторы Ф i и D i .

Чем измерительный сигнал отличается от сигнала? Приведите примеры измерительных сигналов, используемых в различных разделах науки и техники

Измерительный сигнал - это материальный носитель информации, содержащий количественную информацию об измеряемой физической величине и представляющий собой некоторый физический процесс, один из параметров которого функционально связан с измеряемой физической величиной. Такой параметр называют информативным. А сигнал несет количественную информацию только об информативном параметре, а не об измеряемой физической величине.

Примерами измерительных сигналов могут быть

Выходные сигналы различных генераторов (магнитогидродинамического, лазеров, мазеров и др.), трансформаторов (дифференциального, тока, напряжения)

Различные электромагнитные волны (радиоволны, оптическое излучение и др.)

Перечислите признаки, по которым классифицируются измерительные сигналы

По характеру измерения информативного и временного параметров измерительные сигналы делятся на аналоговые, дискретные и цифровые. По характеру изменения во времени сигналы делятся на постоянные и переменные. По степени наличия априорной информации переменные измерительные сигналы делятся на детерминированные, квазидетерминированные и случайные.

Чем аналоговый, дискретный и цифровой сигналы отличаются друг от друга?

Аналоговый сигнал - это сигнал, описываемый непрерывной или кусочно-непрерывной функцией Y a (t), причем как сама эта функция, так и ее аргумент t могут принимать любые значения на заданных интервалах (Y min ; Y max) и (t min ; t max).

Дискретный сигнал - это сигнал, изменяющийся дискретно во времени или по уровню. В первом случае он может принимать в дискретные моменты времени nТ, где Т = const - интервал (период) дискретизации, n = 0; 1; 2; ... - целое, любые значения в интервале (Y min ; Y max)называемые выборками, или отсчетами. Такие сигналы описываются решетчатыми функциями. Во втором случае значения сигнала Yд(t) существуют в любой момент времени t в интервале (t min ; t max) однако они могут принимать ограниченный ряд значений h j = nq, кратных кванту q.

Цифровые сигналы - квантованные по уровню и дискретные по времени сигналы Y ц (nТ), которые описываются квантованными решетчатыми функциями (квантованными последовательностями), принимающими в дискретные моменты времени nТ лишь конечный ряд дискретных значений - уровней квантования h 1 h 2 , ... , h n .

Расскажите о характеристиках и параметрах случайных сигналов

Случайный сигнал - это изменяющаяся во времени физическая величина, мгновенное значение которой является случайной величиной.

Семейство реализаций случайного процесса является основным экспериментальным материалом, на основе которого можно получить его характеристики и параметры.

Каждая реализация является неслучайной функцией времени. Семейство реализаций при каком-либо фиксированном значении времени t o представляет собой случайную величину, называемую сечением случайной функции, соответствующим моменту времени t o . Следовательно, случайная функция совмещает в себе характерные признаки случайной величины и детерминированной функции. При фиксированном значении аргумента она превращается в случайную величину, а в результате каждого отдельного опыта становится детерминированной функцией.

Наиболее полно случайные процессы описываются законами распределения: одномерным, двумерным и Т.д. Однако оперировать с такими, в общем случае многомерными функциями очень сложно, поэтому в инженерных приложениях, каковым является метрология, стараются обойтись характеристиками и параметрами этих законов, которые описывают случайные процессы не полностью, а частично. Характеристики случайных процессов, в отличие от характеристик случайных величин, которые подробно рассмотрены в гл. 6, являются не числами, а функциями. К важнейшим из них относятся математическое ожидание и дисперсия.

Математическим ожиданием случайной функции X(t) называется неслучайная функция

mx(t) = M = хр(х, t)dx,

которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения. Здесь р(х, t) - одномерная плотность распределения случайной величины х в соответствующем сечении случайного процесса X(t). Таким образом, математическое ожидание в данном случае является средней функцией, вокруг которой группируются конкретные реализации.

Дисперсией случайной функции X(t) называется неслучайная функция

Dx(t) = D = 2 p(x, t)dx,

значение которой для каждого момента времени равно дисперсии соответствующего сечения, т.е. дисперсия характеризует разброс реализаций относительно mx(t).

Математическое ожидание случайного процесса и его дисперсия являются весьма важными, но не исчерпывающими характеристиками, так как определяются только одномерным законом распределения. Они не могут характеризовать взаимосвязь между различными сечениями случайного процесса при различных значениях времени t и t". Для этого используется корреляционная функция - неслучайная функция R(t, t") двух аргументов t и t", которая при каждой паре значений аргументов равна ковариации соответствующих сечений случайного процесса:

Корреляционная функция, называемая иногда автокорреляционной, описывает статистическую связь между мгновенными значениями случайной функции, разделенными заданным значением времени ф = t"-t. При равенстве аргументов корреляционная функция равна дисперсии случайного процесса. Она всегда неотрицательна.

На практике часто используется нормированная корреляционная функция

Она обладает следующими свойствами: 1) при равенстве аргументов t и t" r(t, t") = 1; 2) симметрична относительно своих аргументов: r(t,t") = r(t",t); 3) ее возможные значения лежат в диапазоне [-1;1], т.е. |r(t,t")| ? 1. Нормированная корреляционная функция по смыслу аналогична коэффициенту корреляции между случайными величинами, но зависит от двух аргументов и не является постоянной величиной.

Случайные процессы, протекающие во времени однородно, частные реализации которых с постоянной амплитудой колеблются вокруг средней функции, называются стационарными. :Количественно свойства стационарных процессов характеризуются следующими условиями.

* Математическое ожидание стационарного процесса постоянно, Т.е. m х (t) = m х = const. Однако это требование не является существенным, поскольку от случайной функции X(t) всегда можно перейти к центрированной функции, для которой математическое ожидание равно нулю. Отсюда вытекает, что если случайный процесс нестационарен только за счет переменного во времени (по сечениям) математического ожидания, то операцией центрирования его всегда можно свести к стационарному.

* Для стационарного случайного процесса дисперсия по сечениям является постоянной величиной, Т.е. Dx(t) = Dx = const.

* :Корреляционная функция стационарного процесса зависит не от значения аргументов t и t", а только от промежутка ф = t"-t, т.е. R(t,t") = R(ф). Предыдущее условие является частным случаем данного условия, Т.е. Dx(t) = R(t, t) = R(ф = О) = const. Таким образом, зависимость автокорреляционной функции только от интервала "t является единственным существенным условием стационарности случайного процесса.

Важной характеристикой стационарного случайного процесса является его спектральная плотность S(щ), которая описывает частотный состав случайного процесса при щ?0 и выражает среднюю мощность случайного процесса, приходящуюся на единицу полосы частот:

Спектральная плотность стационарного случайного процесса является неотрицательной функцией частоты S(щ)?0. Площадь, заключенная под кривой S(щ), пропорциональна дисперсии процесса. Корреляционная функция может быть выражена через спектральную плотность

R(ф) = S(щ)cosщфdщ.

Стационарные случайные процессы могут обладать или не обладать свойством эргодичности. Стационарный случайный процесс называется эргодическим если любая его реализация достаточной продолжительности является как бы "полномочным представителем" всей совокупности реализаций процесса. В таких процессах любая реализация рано или поздно пройдет через любое состояние независимо от того, в каком состоянии находился этот процесс в начальный момент времени.

Для описания погрешностей используются теория вероятностей и математическая статистика. Однако прежде необходимо сделать ряд существенных оговорок:

* применение методов математической статистики к обработке результатов измерений правомочно лишь в предположении о независимости между собой отдельных получаемых отсчетов;

* большинство используемых в метрологии форму л теории вероятностей правомерны только для непрерывных распределений, в то время как распределения погрешностей вследствие неизбежного квантования отсчетов, строго говоря, всегда дискретны, Т.е. погрешность может принимать лишь счетное множество значений.

Таким образом, условия непрерывности и независимости для результатов измерений и их погрешностей соблюдаются приближенно, а иногда и не соблюдаются. В математике под термином "непрерывная случайная величина" понимается существенно более узкое, ограниченное рядом условий понятие, чем "случайная погрешность" в метрологии.

С учетом этих ограничений процесс появления случайных погрешностей результатов измерений за вычетом систематических и прогрессирующих погрешностей обычно может рассматриваться как центрированный стационарный случайный процесс. Его описание возможно на основе теории статистически независимых случайных величин и стационарных случайных процессов.

При выполнении измерений требуется количественно оценить погрешность. Для такой оценки необходимо знать определенные характеристики и параметры модели погрешности. Их номенклатура зависит от вида модели и требований к оцениваемой погрешности. В метрологии принято различать три группы характеристик и параметров погрешностей. Первая группа - задаваемые в качестве требуемых или допускаемых нормы характеристик погрешности измерений (нормы погрешностей). Вторая группа характеристик - погрешности, приписываемые совокупности выполняемых по определенной методике измерений. Характеристики этих двух групп применяются в основном при массовых технических измерениях и представляют собой вероятностные характеристики погрешности измерений. Третья группа характеристик - статистические оценки погрешностей измерений отражают близость отдельного, экспериментально полученного результата измерения к истинному значению измеряемой величины. Они используются в случае измерений, проводимых при научных исследованиях и метрологических работах.

В качестве характеристик случайной погрешности используют СКО случайной составляющей погрешности измерений и, если необходимо, ее нормализованную автокорреляционную функцию.

Систематическая составляющая погрешности измерений характеризуется:

* СКО неисключенной систематической составляющей погрешности измерений;

* границами, в которых неисключенная систематическая составляющая погрешности измерений находится с заданной вероятностью (в частности, и с вероятностью, равной единице).

Требования к характеристикам погрешности и рекомендации по их выбору приведены в нормативном документе МИ 1317-86 "ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров".