Как определяется пропускная способность канала. Критерии оценки сетей. Каковы принципы организации воздушной радиосвязи и наземной электросвязи
В любой системе связи через канал передается информация. Ее скорость передачи была определена в § 4.2. Как видно из (4.25), эта скорость зависит не только от самого канала, но и от свойств подаваемого на его вход сигнала и поэтому не может характеризовать канал как средство передачи информации. Попытаемся найти способ оценки способности канала передавать информацию. Рассмотрим вначале дискретный канал, через который передаются в единицу времени v символов из алфавита объемом m. При передаче каждого символа в среднем по каналу проходит количество информации
Ширина полосы пропускания
Основной причиной отсутствия полосы пропускания или экспоненциального уменьшения полосы пропускания является конкуренция за пропускную способность между узлами вдоль пути. В этой статье мы продемонстрируем один из способов преодоления этой проблемы за счет использования нескольких каналов с несколькими интерфейсами.
Полученные результаты дают базовую оценку для оценки пропускной способности сетей с несколькими интерфейсами нескольких каналов. В: Конференция по беспроводной связи и сети. . Термин, используемый для обозначения пропускной способности канала связи для информации: узкая полоса пропускания подразумевает медленную или ограниченную связь. В нем описывается пропускная способность подключения пользователей или подключения к серверу. Обычно это меры в битах или байтах в секунду. Узнайте больше в: Организационное обучение с использованием интрасети: социально-культурный подход.
I(A, В) = Н(А) - Н(А|В) = Н(В) - Н(В|А), (4.35)
где А и В - случайные символы на входе и выходе канала. Из четырех фигурирующих здесь энтропий H(A) - собственная информация передаваемого символа определяется источником дискретного сигнала * и не зависит от свойств канала. Остальные три энтропии в общем случае зависят как от источника сигнала, так и от канала.
Физическая характеристика телекоммуникационной системы, указывающая скорость передачи информации. В аналоговых системах он измеряется в циклах в секунду, а в цифровых системах - в бинарных битах в секунду. Полоса пропускания является мерой частотного диапазона и обычно измеряется в герцах. Полоса пропускания связана с пропускной способностью канала для передачи информации.
Теория информации и кодирования
Определяя пропускную способность канала связи, он ссылается на объем данных, который может быть передан в фиксированное время по каналу, он обычно выражается в битах в секунду. Подробнее в: Извлечение большей пропускной способности из витых пар медных проводов.
* (Источником дискретного сигнала в системе связи (см. рис. 1.5) является совокупность источника сообщения и кодера. )
Представим себе, что на вход канала можно подавать символы от разных источников, характеризуемых различными распределениями вероятностей Р(А) (но, конечно, при тех же значениях m и v). Для каждого такого источника количество информации, переданной по каналу, принимает свое значение. Максимальное количество переданной информации, взятое по всевозможным источникам входного сигнала, характеризует сам канал и называется пропускной способностью канала в расчете на один символ
Полоса пропускания - это объем данных, которые можно транспортировать в течение определенного периода времени; он обычно выражается в битах в секунду для цифровой передачи. Рассматривается как скорость передачи данных или объем данных, которые могут переноситься из одной точки в другую за данный период времени. Полоса пропускания обычно измеряется в килобитах в секунду или мегабит в секунду. Узнайте больше в: Пообещание и потенциал технологии потоковых мультимедиа.
Объем данных, которые могут передаваться из одной точки в другую, обычно между веб-сервером и веб-браузером; это мера диапазона частот, передаваемых переданным сигналом. В цифровых системах полоса пропускания полосы пропускания измеряется в терминах разницы между компонентом высокочастотного сигнала и компонентом низкочастотного сигнала. Узнайте больше в: Программное обеспечение Пиратство.
где максимизация * производится по всем многомерным распределениям вероятностей Р(A). Можно также определить пропускную способность С канала в расчете на единицу времени (например, секунду):
* (Если такого максимума не существует (что может быть при бесконечном числе возможных источников), то пропускная способность определяется как наименьшая верхняя грань sup I(А, В), т. е. такая величина, к которой I(А, B) может сколь угодно приблизиться, но не может ее превзойти. )
Это важный параметр для оценки плотности ядра. Гауссова функция является одним из наиболее используемых ядер. В этом случае оценку плотности ядра можно рассматривать как суперпозицию различных функций нормальной плотности, где полоса пропускания является стандартным отклонением нормальной функции плотности. Узнайте больше в: Нечеткий интегральный регрессионный ансамбль ядра и его применение.
Пропускная способность канала связи
Объем данных, которые могут передаваться из одной точки в другую, обычно между веб-сервером и веб-браузером; Это мера диапазона частот, которые занимает передаваемый сигнал. В цифровых системах пропускная способность - это скорость передачи данных в битах в секунду. В аналоговых системах пропускная способность измеряется в терминах разницы между компонентом высокочастотного сигнала и компонентом низкочастотного сигнала.
Равенство (4.37) следует из аддитивности энтропии. В дальнейшем везде, где это особо не оговорено, под пропускной способностью понимать будем пропускную способность в расчете на секунду.
В качестве примера вычислим пропускную способность симметричного канала без памяти, для которого переходные вероятности заданы (3.36). Согласно (4.36)
Диапазон частот в пределах полосы, как требуется для передачи определенного сигнала. скорость, с которой информация может передаваться по линии связи, на устройство и т.д. Компьютерные люди могут использовать термин для возможностей и времени. Например, «недостаточная пропускная способность для выполнения работы» означает недостаточный штат или время для этого.
Пропускная способность электронного пути, такого как линия связи, компьютерная шина или компьютерный канал. Цифровая полоса пропускания - это количество импульсов в секунду, измеренное в битах в секунду. Этот чрезвычайно широкий диапазон определяется силой сигнала и помехами в окружающей среде в любой данный момент. В пакетном режиме может быть выбрана любая из более чем 30 комбинаций полосы пропускания канала, схемы модуляции, скорости коррекции ошибок, расстояния между каналами и количества антенн.
Величина
![]()
в данном случае легко вычисляется, поскольку условная (переходная) вероятность P(b j |a i) принимает только два значения: p/(m-1), если b j ≠a i и 1-р, если b j = a i . Первое из этих значений возникает с вероятностью р, а второе - с вероятностью 1-р. К тому же, поскольку рассматривается канал без памяти, результаты приема отдельных символов независимы друг от друга. Поэтому
Полоса пропускания канала, необходимая для передачи сигналов различных типов, с использованием различных схем обработки. Каждый наблюдаемый на практике сигнал может быть выражен как сумма синусоидальных компонентов различных частот. График амплитуды и частоты составляет одну особенность частотного спектра. Разница между самой высокой и самой низкой частотами частотных составляющих значительных амплитуд в спектре называется полосой пропускания сигнала, выраженной в единице частоты, герц. Каждый коммуникационный носитель способен передавать полосу частот с разумной точностью.
Следовательно, Н(В|А) не зависит от распределения вероятности в ансамбле А, а определяется только переходными вероятностями канала. Это свойство сохраняется для всех моделей канала с аддитивным шумом.
Подставив (4.38) в (4.37), получим
Поскольку в правой части только член Н (В) зависит от распределения вероятностей Р(А), то максимизировать необходимо его. Максимальное значение Н (В) согласно (4.6) равно log m и реализуется оно тогда, когда все принятые символы b j равновероятны и независимы друг от друга. Легко убедиться, что это условие удовлетворяется, если входные символы равновероятны и независимы, поскольку в этом случае
Качественно говоря, разница между самой высокой и самой низкой частотой компонентов в полосе, по которой коэффициент усиления канала остается достаточно постоянным, называется полосой пропускания канала. Очевидно, что для передачи сигнала с разумной точностью по каналу связи полоса пропускания канала должна соответствовать и быть, по меньшей мере, равной ширине полосы сигнала. Однако надлежащее кондиционирование сигнала, такое как модуляция или кодирование, может увеличивать или уменьшать полосу пропускания обработанного сигнала.
Что будем делать с полученным материалом
Таким образом, можно передавать информацию о сигнале по каналу ширины полосы, большему или меньшему, чем у исходного сигнала. Амплитудная модуляция с двойными боковыми полосами, например, удваивает ширину полосы сигнала. Амплитудная модуляция с одной боковой полосой, с другой стороны, требует такой же пропускной способности, что и для исходного сигнала. С другой стороны, в широковещательной частотной модуляции ширина полосы аудиосигнала составляет 15 кГц, но соответствующая полоса частот с частотной модуляцией составляет 200 кГц.
При этом Н(В) = log m и
Отсюда пропускная способность в расчете на единицу времени
Для двоичного симметричного канала (m = 2) пропускная способность в двоичных единицах в единицу времени
С = v (4.42)
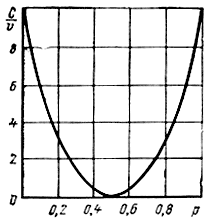
Зависимость C/v от р согласно (4.42) показана на рис. 4.3.
При р = 1/2 пропускная способность двоичного канала С = 0, поскольку при такой вероятности ошибки последовательность выходных двоичных символов можно получить совсем не передавая сигналы по каналу, а выбирая их наугад (например, по результатам бросания монеты), т. е. при р=1/2 последовательности на выходе и входе канала независимы. Случай С = 0 называют обрывом канала. То, что пропускная способность при р = 1 в двоичном канале такая же, как при р=0 (канал без шумов), объясняется тем, что при р = 1 достаточно все выходные символы инвертировать (т. е. заменить 0 на 1 и 1 на 0), чтобы правильно восстановить входной сигнал.
Этот результат предполагает белый гауссовский шум, который является наихудшим видом шума с точки зрения помех. Следствием уравнения Шеннона является то, что если сигнал правильно обрабатывается для увеличения его полосы пропускания, обработанный сигнал становится более защищенным от помех или шума по каналу. Это означает, что увеличение полосы пропускания передачи может подавлять шум в полученном сигнала, что приводит к получению более качественного сигнала на приемнике. Частотная модуляция и импульсно-кодовая модуляция являются двумя примерами широкополосных схем, где пропускная способность передачи может быть увеличена по мере необходимости для подавления шума.
Пропускная способность непрерывного к а н а- л а вычисляется аналогично. Пусть, например, канал имеет ограниченную полосу пропускания шириной F. Тогда сигналы U(t) и Z{t) соответственно на входе и выходе канала по теореме Котельникова определяются своими отсчетами, взятыми через интервал 1/(2F), и поэтому информация, проходящая по каналу за некоторое время Т, равна сумме количества информации, переданной за каждый такой отсчет * . Пропускная способность канала на один такой отсчет
Широкополосная связь также используется, чтобы сделать коммуникацию менее уязвимой для заклинивания и незаконного приема с использованием так называемого сигнала расширенного спектра. Видеть. И Интернет является домом для руководителей социальных сетей. Чтобы обеспечить такое же внутреннее принятие, как среди блоггеров и онлайн-мультипликаторов, Менеджеры социальных сетей должны поддерживать как минимум внутреннюю связь. Как и с какими мерами это может быть достигнуто, этот вклад призван дать ответ.
Во многих случаях внутренняя коммуникация в компаниях не является очень важным фактором. Главный фасад, фасад наружу. и, таким образом, выходят за рамки чистого управления контентом и приверженности официальным каналам компании, могут быть реализованы только в том случае, если они сопровождаются продуманной и непрерывной внутренней связью.
Здесь U и Z - случайные величины - сечения процессов U(t) и Z(t) на входе и выходе канала соответственно и максимум берется по всем допустимым входным сигналам, т. е. по всем распределениям U.
* (Можно вместо ряда Котельникова использовать разложение сигналов по- любому ортогональному базису и рассмотреть количество передаваемой информации на каждый член ряда. )
Для успешной коммуникационной стратегии в компании менеджеры социальных сетей должны определять различные целевые группы, активно участвовать в лодке и регулярно предоставлять соответствующую информацию о своих проектах. Диапазон адресатов варьируется от высшего руководства до собственного отдела.
Информация в компании
Почему так важна внутренняя коммуникация вокруг стратегии и деятельности в социальных сетях. Информационный поток: создать процессы доставки в компании, чтобы важная информация также могла доходить до групп диалога в социальной сети. Прозрачность: информируйте коллег о цифровых проектах компании и показывайте, какие темы продвигаются вперед. Диалог: Участие в обсуждении с коллегами И поощрять коллег к участию, например, путем активного участия в качестве блоггера.
- Личный брендинг: видимый для менеджмента и коллег.
- Работа по убеждению: повышение признания для цифровых тем.
Пропускная способность С определяется как сумма значений Сотсч, взятая по всем отсчетам за секунду. При этом, разумеется, дифференциальные энтропии в (4.43) должны вычисляться с учетом вероятностных связей между отсчетами.
Вычислим, например, пропускную способность непрерывного канала без памяти с аддитивным белым гауссовским шумом, имеющим полосу пропускания шириной F, если средняя мощность сигнала (дисперсия U) не превышает заданной величины Р с. Мощность (дисперсию) шума в полосе F обозначим Р ш. Отсчеты входного и выходного сигналов, а также шума N связаны равенством
Каковы принципы организации воздушной радиосвязи и наземной электросвязи
Чтобы продвинуть этот вопрос. Есть тысячи в компании и канал связи, через который менеджеры социальных сетей могут сделать свои проекты известными и конкурировать за свое дело. Несколько примеров. Ведомственные собрания: важно регулярно обновлять информацию, даже если это всего лишь пять минут. Это улучшает восприятие ваших коллег, повышает вашу видимость и увеличивает признание для темы социальных сетей.
Информационный бюллетень: Коллеги могут получать информацию о текущих социальных проектах и контенте через регулярные промежутки времени с помощью бюллетеня. Возможно, уже есть информационный бюллетень, по которому может переключаться Менеджер социальных медиа.
Z = U + N. (4.44)
Так как N имеет нормальное распределение с нулевым математическим ожиданием, то и условная плотность вероятности w(z|u) при фиксированном и будет также нормальной - с математическим ожиданием и и дисперсией Р ш.
Найдем пропускную способность на один отсчет (4.43):
Согласно (4.34) дифференциальная энтропия h(Z|U) нормального распределения w(Z|U) не зависит от математического ожидания и равна
Интранет: официальные социальные веб-презентации компании могут быть интегрированы на домашнюю страницу интрасети. Журнал сотрудников: Отдельный раздел в журнале сотрудников стоит того. Таким образом, менеджеры социальных сетей могут информировать коллег о своих проектах или новых тенденциях в мире социальной сети или начинать звонки, например, чтобы завоевать новых блоггеров.
Скорость передачи информации
Например, на болтовне руководители социальных сетей могут создавать свои собственные группы, указывать свои темы в других группах, загружать важные документы, запускать опросы и т.д. Кафетерий, кафетерий, зоны для курения: Как вы знаете, самые социальные места в компании, где вы можете встретиться и пообщаться. Это возможность наладить контакты, связаться и получить обратную связь. В общем капучино некоторые идеи уже созданы для хорошего блога!
![]()
Поэтому для нахождения С отсч следует найти такую плотность распределения w(U), при которой максимизируется h(Z). Из (4.44) учитывая, что U и N - независимые случайные величины, имеем для дисперсий:
D(Z) = D(U) + D(N) = P c + P ш. (4.45)
Таким образом, дисперсия Z фиксирована, так как Р с и Р ш заданы. Как было отмечено (см. стр. 114), при фиксированной дисперсии максимальная дифференциальная энтропия обеспечивается нормальным распределением. Из (4.44) видно, что при нормальном одномерном распределении U распределение Z будет также нормальным и, следовательно, обеспечивается максимум дифференциальной энтропии (4.34):
Переходя к пропускной способности С в расчете на секунду, заметим, что информация, переданная за несколько отсчетов, максимальна в том случае, когда отсчеты сигналов независимы. Этого можно достичь, если сигнал U(t) выбрать так, чтобы его спектральная плотность была равномерной в полосе F. Как было показано в § 2.2 [см. (2.48)], отсчеты, разделенные интервалами, кратными 1/(2F), взаимно некоррелированы, а для гауссовских величин некоррелированность означает независимость.
Поэтому пропускную способность С (за секунду) можно найти, сложив пропускные способности (4.46) для 2F независимых отсчетов:
С = 2FC отсч = F log (1 +Р с /Р ш). (4.47)
Она реализуется, если U(t) - гауссовский процесс с равномерной спектральной плотностью в полосе частот F (квазибелый шум).
Из (4.47) видно, что если бы мощность сигнала Р с не была ограничена, то пропускная способность была бы сколь угодно большой. Пропускная способность равна нулю, если отношение сигнал-шум Р с /Р ш в канале равно нулю. С ростом этого отношения пропускная способность увеличивается неограниченно, однако медленно, вследствие логарифмической зависимости.
Соотношение (4.47) часто называют формулой Шеннона. Эта формула имеет важное значение в теории информации, так как определяет зависимость пропускной способности рассматриваемого непрерывного канала от таких его технических характеристик, как ширина полосы пропускания и отношение сигнал-шум. Формула Шеннона указывает на возможность обмена полосы пропускания на мощность сигнала, и наоборот. Однако поскольку С зависит от F линейно, а от Р с /Р ш - по логарифмическому закону, компенсировать возможное сокращение полосы пропускания увеличением мощности сигнала, как правило, не выгодно. Более эффективным является обратный обмен мощности сигнала на полосу пропускания.
Заметим, что при Р c /P ш >>1 выражение (4.50) совпадает с характеристикой (1.2), названной в § 1.2 емкостью (объемом) канала.
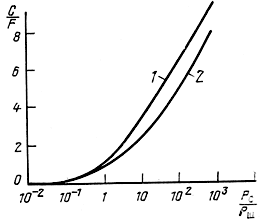
Следует подчеркнуть, что формула Шеннона (4.47) справедлива только для канала с постоянными параметрами и аддитивным гауссовским белым (или квазибелым) шумом. Если распределение аддитивной помехи не является нормальным или же ее спектр неравномерен в полосе пропускания канала, то его пропускная способность больше, чем вычисленная по формуле (4.47). Мультипликативные помехи (замирания сигнала) обычно снижают пропускную способность канала.
На рис. 4.5 показаны зависимости С/F от среднего отношения Р с /Р ш для канала с постоянными параметрами (1) и канала с рэлеевскими замираниями (2). Из анализа кривых следует, что медленные рэлеевские замирания уменьшают пропускную способность канала не более чем на 17%.
В любой системе связи через канал передается информация. Скорость передачи информации была определена в § 2.9. Эта скорость зависит не только от самого канала, но и от свойств подаваемого на его вход сигнала и поэтому не может характеризовать канал как средство передачи информации. Попытаемся найти способ оценки способности канала передавать информацию. Рассмотрим вначале дискретный канал, через который передаются в единицу времени символов из алфавита объемом При передаче каждого символа в среднем по каналу проходит следующее количество информации [см. (2.135) и (2.140)]:
где случайные символы на входе и выходе канала. Из четырех фигурирующих здесь энтропий -собственная информация передаваемого символа - определяется источником дискретного сигнала и не зависит от свойств канала. Остальные три энтропии в общем случае зависят как от источника сигнала, так и от канала.
Представим себе, что на вход канала можно подавать символы от разных источников, характеризуемых различными распределениями вероятностей (но, конечно, при тех же значениях . Для каждого такого источника количество информации, переданной по каналу, принимает свое значение. Максимальное количество переданной информации, взятое по всевозможным
источникам входного сигнала, характеризует сам канал и называется пропускной способностью канала. В расчете на один символ
где максимизация производится по всем многомерным распределениям вероятностей Можно также определить пропускную способность С канала в расчете на единицу времени (секунду):
Последнее равенство следует из аддитивности энтропии. В дальнейшем везде, где это особо не оговорено, будем под пропускной способностью понимать пропускную способность в расчете на секунду.
В качестве примера вычислим пропускную способность симметричного канала без памяти, для которого переходные вероятности заданы формулой (3.36). Согласно (3.52) и (3.53)
![]()
Величина в данном случае легко вычисляется, поскольку условная переходная вероятность принимает только два значения: , если еслн Первое из этих значений возникает с вероятностью а второе с вероятностью К тому же, поскольку рассматривается канал без памяти, результаты приема отдельных символов независимы друг от друга. Поэтому
Следовательно, не зависит от распределения вероятности В, а определяется только переходными вероятностями канала. Это свойство сохраняется для всех моделей канала с аддитивным шумом.
Подставив (3.56) в (3.55), получим
Поскольку в правой части только член зависит от распределения вероятностей то максимизировать необходимо его. Максимальное значение согласно (2.123) равно и реализуется оно тогда, когда все принятые символы равновероятны и независимы друг от друга. Легко убедиться, что это условие удовлетворяется, еслн входные символы равновероятны и независимы, поскольку
При этом и
Отсюда пропускная способность в расчете на секунду
Для двоичного симметричного канала пропускная способность в двоичных единицах в секунду
Зависимость от согласно (3.59) показана на рис. 3.9.
При пропускная способность двоичного канала поскольку при такой вероятности ошибки последовательность выходных двоичных символов можно получить, совсем не передавая сигналы по каналу, а выбирая их наугад (например, по результатам бросания монеты), т. е. при последовательности на выходе и входе канала независимы. Случай называют обрывом канала. То, что пропускная способность при в двоичном канале такая же, как при (канал без шумов), объясняется тем, что при достаточно все выходные символы инвертировать (т. е. заменить 0 на 1 и 1 на 0), чтобы правильно восстановить входной сигнал.
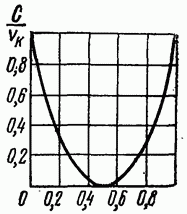
Рис. 3.9. Зависимость пропускной способности двоичного симметричного канала без памяти от вероятности ошибочного приема символа
Пропускная способность непрерывного канала вычисляется аналогично. Пусть, например, канал имеет ограниченную полосу пропускания шириной Тогда сигналы на входе и выходе канала по теореме Котельникова определяются своими отсчетами, взятыми через интервал и поэтому информация, проходящая по каналу за некоторое время равна сумме количеств информации, переданных за каждый такой отсчет. Пропускная способность канала на один такой отсчет
Здесь случайные величины - сечения процессов на входе и выходе канала и максимум берется по всем допустимым входным сигналам, т. е. по всем распределениям .
Пропускная способность С определяется как сумма значений Сотсч» взятая по всем отсчетам за секунду. При этом, разумеется, дифференциальные энтропии в (3.60) должны вычисляться с учетом вероятностных связей между отсчетами.
Вычислим, например, пропускную способность непрерывного канала без памяти с аддитивным белым гауссовским шумом, имеющим полосу пропускания шириной если средняя мощность сигнала (дисперсия не превышает заданной величины Мощность (дисперсию) шума в полосе обозначим Отсчеты входного и выходного сигналов, а также шума связаны равенством
н так как имеет нормальное распределение с нулевым математическим ожиданием, то и условная плотность вероятности при фиксированном и будет также нормальной - с математическим ожиданием и и дисперсией Найдем пропускную способность на один отсчет:
Согласно (2.152) дифференциальная энтропия нормального распределения не зависит от математического ожидания и равна Поэтому для нахождения нужно найти такую плотность распределения при которой максимизируется Из (3.61), учитывая, что независимые случайные величины, имеем
Таким образом, дисперсия фиксирована, так как заданы. Согласно (2.153), при фиксированной дисперсии максимальная дифференциальная энтропия обеспечивается нормальным распределением. Из (3.61) видно, что при нормальном одномерном распределении распределение будет также нормальным и, следовательно,
Переходя к пропускной способности С в расчете на секунду, заметим, что информация, переданная за несколько отсчетов, максимальна в том случае, когда отсчеты сигналов независимы. Этого можно достичь, если сигнал выбрать так, чтобы его спектральная плотность была равномерной в полосе Как было показано в отсчеты, разделенные интервалами, кратными взаимно некоррелированны, а для гауссовских величин некоррелированность означает независимость.
Поэтому пропускную способность С (за секунду) можно найти, сложив пропускные способности (3.63) для независимых отсчетов:
Она реализуется, если гауссовский процесс с равномерной спектральной плотностью в полосе частот (квазибелый шум).
Из формулы (3.64) видно, что если бы мощность сигнала не была ограничена, то пропускная способность была бы бесконечной. Пропускная способность равна нулю, если отношение сигнал/шум в канале равно нулю. С ростом этого отношения пропускная способность увеличивается неограниченно, однако медленно, вследствие логарифмической зависимости.
Соотношение (3.64) часто называют формулой Шеннона. Эта формула имеет важное значение в теории информации, так как определяет зависимость пропускной способности рассматриваемого непрерывного канала от таких его технических характеристик, как ширина полосы пропускания и отношение сигна/шум. Формула Шеннона указывает на возможность обмена полосы пропускания на мощность сигнала и наоборот. Однако поскольку С зависит от линейно, а от по логарифмическому закону, компенсировать возможное сокращение полосы пропускания увеличением мощности сигнала, как правило, нецелесообразно. Более эффективным является обратный обмен мощности сигнала на полосу пропускания.